“程序需要对非常难以计算的数值进行缓存,使用空间换取时间”
相信大多数写过程序的都知道这一点,但是如果没有真正对比一下是不会留下深刻印象的。
今天看《SICP》里提到斐波那契函数是树形的递归调用,突然想到计算斐波那契数可以非常好地显示缓存的威力,斐波那契数求法如下
unsigned long long fib(unsigned int n){
if ( n < 2 )
return n;
return fib(n-1) + fib(n-2);
}
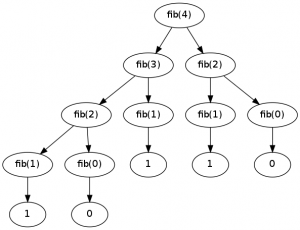
这是一个递归的函数,对于参数为4的调用树见下图:
从图中可以看出fib(4)函数会调用fib(3)和fib(2),然后fib(3)又会调用fib(2)和fib(1),问题就出在这:fib(4)调用了fib(2)一次,而fib(3)也调用了fib(2)一次,这样对于每次对fib函数的调用都会产生两棵完全相同的子树,这样的计算完全不划算,要计算的数值越大,重复的子数也就越多,但如果使用缓存效率就会有巨大的提升,所谓缓存就是先不进行计算,查看缓存中是否已经有计算好了的值,如果有就直接拿来用,没有再进行计算,并将结果存入缓存再返回。使用缓存的fib函数如下:
unsigned long long fib_cache(unsigned int n){
static unsigned long long *cache = NULL;
if ( n < 2 )
return n;
if ( cache == NULL ) {
cache = calloc(n - 1, sizeof(unsigned long long));
memset(cache, n - 1, 0);
}
if ( cache[n - 2] == 0 )
cache[n - 2] = fib_cache(n-1) + fib_cache(n-2);
return cache[n - 2];
}
使用缓存后计算5000的斐波那契数也是瞬间完成,但是没有使用缓存的算法连50都让人等不下去了。
这便是缓存的威力。