最近看了下逻辑编程,据说逻辑编程最牛的是prolog,但是没空再学一门语言了,而且看到clojure中刚好有core.logic的这个库,而且可以拿这个库写《The Reasoned Schemer》中的例子,所以就直接用这个库来学了。
准备工作
先把
[org.clojure/core.logic "0.8.8"]
放到你的project.clj的依赖中,然后在repl中运行
user=> (require '[clojure.core.logic :as logic])
使用这个库的代码一般像
user=> (logic/run 1 [x] (logic/== x 100))
(100)
其中1表明要的结果数量,因为约束条件不一定只有一种可能;x表示需要对哪个变量进行求解;而(logic/== x 100)就是所谓的goal了,整个逻辑编程的推动力就是满足goal。所以上面的代码读作“告诉我x的一个值让其满足x等于100”。因此表达式的值就是(100),是一个包含值100的链表,这就是x应该取的值,因为我们限制结果数量为1,所以结果链表的长度不会大于1,当然,如果没有满足条件的值长度就为0。
因为logic/run的body内部必须是goal而非普通表达式,一般的表达式都不能用在里面。所以这个库另外提供了一些针对链表操作的primitive,像firsto,resto和conso这样和clojure内置的first,rest和cons对应,加了一个o以示区别,而且与内置函数相比都多了一个参数——用于接受类似于内置函数的返回值。
比如:
user=> (logic/run 1 [x] (logic/conso 1 [2 3 4] x))
((1 2 3 4))
意思是求让x满足等于(cons 1 [2 3 4])的值,所以结果也合乎想象,这种调用方式乍看起来感觉很像C语言中的传入一个指针,函数往这个地址中写数据来影响外部环境而不用写全局变量。但是其实不是这样理解,这种形式主要是为了让你可以指定一个结果,让库帮忙推导可以得出这种结果的初始状态,像:
user=> (logic/run 1 [x] (logic/conso 1 x '(1 2 3)))
((2 3))
这里就求出了x必须是’(2 3)才能满足(= (cons 1 x) '(1 2 3))
《The Reasoned Schemer》前面几章讲的都是对链表的操作,完全没涉及数学计算,但是第7、8章就描述了如何使用链表来表示数字的计算,方式类似于电子的门电路,然后组成全加器,最后组成高阶的+o、*o这些内置函数。不知道真实计算会用什么方法,可能会内置数学的一些操作吧,因为用链表来表示实在是太低效了,这样的用法只是适合理解一些原理。
逻辑编程最基本的内容差不多就是这些了,抽象出来了一个goal,让编程者可以只需要编写规则,让程序自动求解,会大量用于Automated reasoning。
内部原理
我对逻辑编程感兴趣的原因之一就是没法理解它是怎么实现的,甚至之前完全不知道逻辑编程是怎么样的一种形式,幸好《The Reasoned Schemer》不仅仅讲了怎么用,还讲了内部的实现原理。
其实逻辑编程最基本的操作就是==操作了,用它来让两个值相等,然后求出满足这些等式的具体变量值,比如(== x y)和(== x 100)以及(== '(x y) '(1 2))等等,而这个操作最终依赖于unify函数,这也是我在做Typed Clojure项目之前查类型系统资料时完全没法理解的unification,也就是合一,但是书中给的代码就很好理解了。这里吐槽一下wiki,有些原理查wiki完全看不懂,它倾向于把一个道理讲得很细,但是在这众多的细节中很容易抓不到重点,其实wiki里面那么多废话完全就可以用几行代码来理解。
goal在内部是一个函数,接受一个substitution,返回false或一个新的substitution,false表示合一失败,而返回substitution表示满足该goal,并且这个新的substitution也包含了满足该goal的新条件。goal一般不需要用户自己编写,一般是使用==让系统生成。而substitution可以理解成一个符号到值的映射,当然也可以是符号到符号的映射。比如给goal (== x y)一个空的substitution,就会产生一个{x -> y}这样的substitution,而如果这个substitution再传递给(== x 10)这样的goal,那么就会产生{x -> 10, y -> 10}这样的映射。
它的内部原理其实就是相当于将需要求解的goal转化成了一个树,然后让程序自动遍历这个树而已。
比如
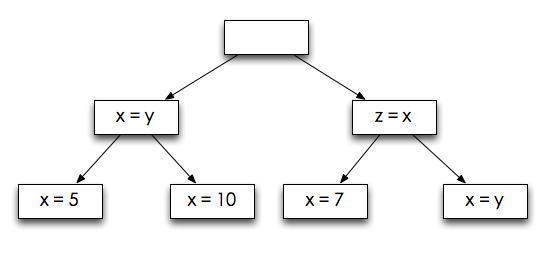
其中每个conde条目都是在创建一个树的分支,conde在书中有详细描述,这里就不详细介绍了,简单来说它就相当于clojure里的cond。因此上面的代码实际上相当于遍历这样的树:
表达式的结果为([5 5 _0] [7 _0 7] [10 10 _0] [_0 _0 _0]),其中_0表示可以为任意值,这样的每一个结果正好对应从根到叶子节点所积累的条件,所以有4个叶子节点就有4个结果,虽然我们请求5个结果。需要注意的是叶子节点不一定会满足条件,如果不满足则积累的substitution会被丢弃,就不会生成结果,而且一旦生成的结果满足了我们的需求量就不会继续计算,这也有点像lazy evaluation。
所以逻辑编程的意义就在于不需要写树的遍历,让程序自动遍历罢了。不过这也是相当有用的一个抽象了,完全开创了一个新的编程模型。
实际用途
我知道的其中一个用途,也是我想要了解逻辑编程的原因,就是因为它可以用于类型系统的类型推导,比如haskell里面的
Prelude> map id [1, 2, 3]
[1,2,3]
这样的函数调用,其中map的类型为map :: (a -> b) -> [a] -> [b],id的类型为id :: a -> a,而[1, 2, 3]的类型为[Num],编译器需要怎么推断map id [1, 2, 3]的类型呢?这里困难的地方就在于map和id都是多态函数,所谓多态函数就是函数类型并不是确定的,需要用类型变量来确定真实的类型,因为map并不关心第一个参数的参数和返回值类型。如果在静态类型语言中不能用类型变量会非常痛苦,就像java那样还需要为int,double写各种版本的函数。但是这样的类型变量就会让类型检查很不方便,因为不能直接比较了,而如果让程序员在每个多态函数的调用部分都加上类型注释又显得太不智能,所以必须要编译器自己去做这样的类型推导。整个推导的过程就需要用到逻辑编程里的合一,也就是unification。
这里详细解释一下整个推导过程。先解释一下函数的类型标记,map的(a -> b) -> [a] -> [b],这样的标记的意思表示map函数接受两个参数,第一个参数是参数类型为类型变量a,返回类型为类型变量b的函数,map的第二个参数是类型为类型变量a的链表,而map的返回值的类型为类型变量b。所以,如果类型变量a为Int,而类型变量b为String,那么map的第一个参数就必须是接受Int,返回String的函数,第二个参数必须是Int的链表,返回值是String的链表。
而id这个函数接受什么返回什么,就是clojure中的identity,所以类型为a -> a,为了之后的叙述方便把它改为c -> c。
所以在检查表达式map id [1, 2, 3]的类型时需要先推断出所有的类型变量所代表的真正类型,先推断第一个参数,可以很容易得到{a -> c, b -> c}这样的映射,之后再检查第二个参数,同时考虑已经得到的信息就会得到{a -> Num, b -> Num, c -> Num}这样的映射,过程中没有类型变量的冲突,所以整个检查成功,而且可以得知整个表达式的返回值是Num的链表。
考虑一个类型错误的表达式map odd ["a", "b", "c"],其中odd函数的类型为Num -> Bool,不是多态函数,这里推导出第一个参数时会得出{a -> Num, b -> Bool}这样的映射,推导第二个参数时会得出{a -> String},这和前面推导出的结果相冲突,所以合一失败,也就导致了类型检查失败。